This is a class summary of AAI5003, 2021 spring semester lectured by Jinyoung Yeo at Yonsei University.
Sequence Data
What is sequence data? It is data whose order matters. Many problems that people are trying to solve using deep learning consist of sequence data: speech recognition, natural language processing….
For example, in machine translation, it is difficult to understand a single word without its context, a set of neighboring words. Thus, we should consider previous/historical data to better understand the word.
However, NN/CNN cannot deal with sequential properties (except word embedding).
What is RNN?
This is a simple form of NN, called Vanilla Feed Foward Network (Vanilla NN). Vanilla NN aggregates all features into a fixed size. It does not reflect time dependent features of sequential data well, resulting in poor model performance.
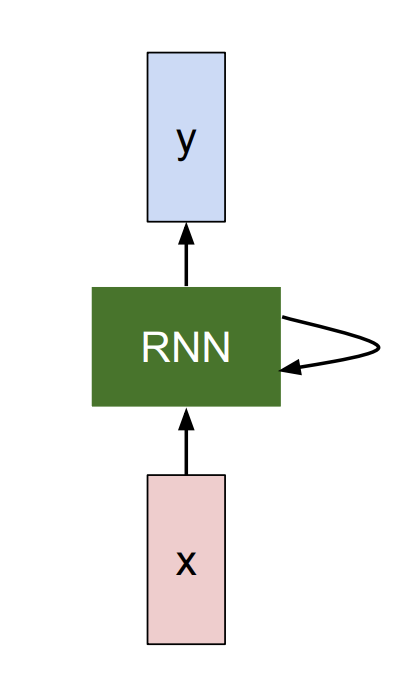
On the other hand, Recurrent Neural Networks (RNN) accumulated representations step by step in the order of sequential data. By doing so, the model is aware of temporal dependency. Note that
The internal state (green) keeps being updated so the same function and set of parameters are re-used at every time step
RNN Applications
- Speech Recognition
- Machine Translation
- Image/Audio Captioning
- Sentiment Analysis
… lots of applications!
RNN Equations
As the term, “recurrent” neural networks, implies, we need a previous hidden state($h_{t_1}$) and input data $x$ at time step $t$ to predict $y_t$.
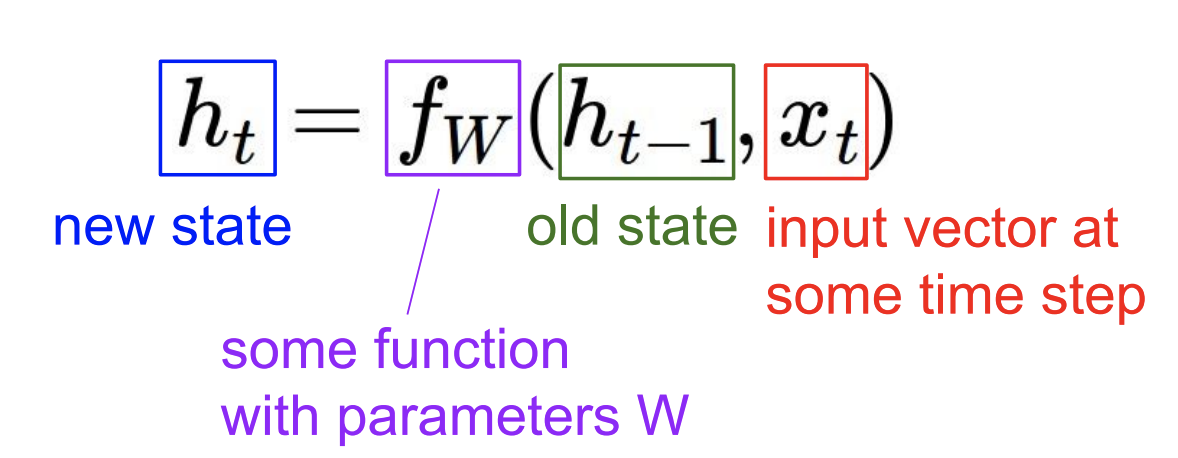
Precisely,
$h_t = f_w(h_{t-1}, x_t)$
$h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$
$y_t = W_{hy}h_t$
Where $h$ is a single hidden vector, being a part of the hidden state.
Deep into the weight matrix, W
The keypoint to understand RNN, I think, is that we re-use the weight matrix. That means we do not specialize W for the given term x.
Let’s think about a simple example.
I am happy
If we want to know the meaning of “happy”, $x_t$, there are two ways to do so: the term itself or its context. For the target word “happy”, its context words are “I” and “am”.
Vanilla NN independently encodes the term regardless of its neighboring words, but in RNN, we encode “happy” conditioned on contexts.
In other words, using the equations describe above,
$h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$
this can be divided into two parts:
Encoding context ($W_{hh}h_{t_1}$) + Encoding the term itself ($W_{xh}x_t$)
W contributes to changing dimensionality and representation as well.
Because of its recurrence property, a starting point is so crucial that it may affect the overall performance. (I will cover some significant research papers dealing with this problem later.)
In backpropagation, RNN might be faced with vanishing gradient problems. LSTM, a developed form of RNN with additive interactions, can control the gradient vanishing problem. See more details about LSTM in the next posting :)